Spiral de l'Ekman
La spiràl de l’Ekman (ciamada inscì per via del mòmm de l’oceanografo svedés Vagn Walfrid Ekman[1]) l’indica ‘na struttura de corrent o vent intorna de on lìmit orizzontal indoe la direzion del fluss la gira in fonzión de la distanz del lìmit medèsim.
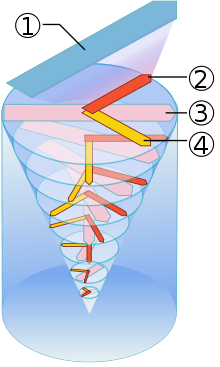
1. Vent
2. Fòrza esercitada de sora
3. Direzion de la corrent
4. Fòrza del Coriolis
Descrizion de la spiral de l’Ekman in di oceani
ModifegaLa spiral l’è na conseguenza de la fòrza del Coriolis che la pròvoca on moviment di oggètt che hànn ‘na velocità maggiora de zero vèrso drizza in del'emisfero nòrd e vèrso sinistra in del'emisfero sud. Per quèst quand che i vent boffen sora la superfice di oceani (in manera "continua"), in del'emisfero nòrd, el se créa on stràt superficiàl ciamàa strat de l’Ekman, che ‘l po’ andà de 45 m fin a 300 m (in di miglior condizion), a segonda di caratteristich del bascì idrich, de la fòrza del vent e de la latitudin. La corrent de superfice, in quèst strato chì, la se moeuv a 45° vèrs drizza rispètt a la direzion del vent.
Quand che l'acqua in su la superfice ruza l’acqua che la stà de sòta, a caosa di fòrz de attrito quèsta chì la se moeuv anmò pussée vèrs dètra rispètt a la direzion del vent, e inscì per tucc i strat pussée de bass. A ‘ndà giò in profondità, per via de la deviazion de la corrent, la velocità de l’acqua la diminuìss semper pussée fin a diventà nagòtt.
El fenòmen el pò vèss osservà in del mar in di corrent marin e in di deriv di giazzee in superfice.
On alter fenòmen present in del strat de l’Ekman a l’è el traspòrt de Ekman. [2] [3] [4] [5] [6] [7] [8] [9] [10] [11]
La spiral de l’Ekman in meteorologia
ModifegaEl modèll del vent de l’Ekman el servìss anca in meteorologia de già che con l’andà giò in quòta denter in del strat de messedada el vent el diminuìss la soa intensità e ‘l compìss on girament a comenzà de la soa direzion iniziàl, che la correspond al vent geostròfich vèrs ‘na direzion che la taja i isòbar cont ‘n’àngol che ‘l tend semper pussée a 90°C e ‘l gh’hà on vèrs contrari de quèll del gradient. Cont el vesinàss a la superfice terrèster, de sorapù, l’attrito el se sent semper pussée, el mòto el va semper pù adasi e de conseguenza la diminìss anca la fòrza del Coriolis.[12]
Vos correlaa
ModifegaRiferiment
Modifega- ↑ Ekman, V.W., 1905. On the influence of the earth's rotation on ocean currents. Arch. Math. Astron. Phys. 2, No. 11
- ↑ Colling, A., Ocean Circulation, Open University Course Team. Second Edition. 2001. ISBN 978-0-7506-5278-0
- ↑ Knauss, J.A., Introduction to Physical Oceanography, Waveland Press. Second Edition. 2005. ISBN 978-1-57766-429-1
- ↑ Mann, K.H. and Lazier J.R., Dynamics of Marine Ecosystems, Blackwell Publishing. Third Edition. 2006. ISBN 978-1-4051-1118-8
- ↑ Pond, S. and Pickard, G.L., Introductory Dynamical Oceanography, Pergamon Press. Second edition. 1983. ISBN 978-0-08-028728-7
- ↑ Sverdrup, K.A., Duxbury, A.C., Duxbury, A.B., An Introduction to The World's Oceans, McGraw-Hill. Eighth Edition. 2005. ISBN 978-0-07-294555-3
- ↑ Ekman, V.W., 1905. On the influence of the earth's rotation on ocean currents. Arch. Math. Astron. Phys. 2, No. 11
- ↑ Gill, A.E. (1982). Atmosphere-Ocean Dynamics. Academic Press Inc. New York, London, Tokyo, ISBN 0-12-283520-4
- ↑ Fennel, W. and H.-U. Lass, 1989. Analytical Theory of Forced Ocean Waves. Akademie-Verlag-Berlin, ISBN 3-05-500421-3
- ↑ Weller, R.A., Plueddemann, A.J., 1996. Observations of the vertical structure of the oceanic boundary layer. J. Geophys. Res., 101, C4, 8789-8806
- ↑ Schudlich, R.R., Price, J.F., 1998. Observations of Seasonal Variation in the Ekman Layer. J. Phys. Oceanogr., 28, 6, 1187-1204
- ↑ Mario Giuliacci (2010). Manuale di meteorologia (in italian). Alpha Test, 327-330. ISBN 88-483-1168-7.